sandbox/lopez/lamb.c

    Stokes flow around an sphere

    The analitical solution of a viscous dominant horizontal flow of magnitude U_o around an sphere of radius a is due to Horace Lamb.

    The solution can be written in terms of the stream function as:

    \displaystyle \Psi (r, \theta) = \frac{U_o \sin^2 \theta}{2} \left(r^2 - \frac{3ar}{2} + \frac{a^3}{2r}\right)

    where we have used polar coordinates.

    The velocities are obtained simply deriving the above expressions,

    \displaystyle u_r(r,\theta) = \cos \theta \left( 1 +\frac{1}{2r^3} - \frac{3}{2r} \right) \quad u_\theta(r,\theta) = -\sin \theta \left( 1 -\frac{1}{4r^3} - \frac{3}{4r} \right)

    where we have made dimensionless the velocity with U_o and r with the radius a. We will use the centered Navier-Stokes solver with embedded boundaries to reproduce his result.

    #include "embed.h"
#include "axi.h"
#include "navier-stokes/centered.h"
#include "view.h"

    The computational domain is an square box of width W where we insert an sphere of dimensionless radius 1. We set the sphere in a very large box to minimize the influence of the location of the far field boundary (W/a \simeq 100).

    #define W 100

scalar un[];
int LEVEL = 10;

int main() {
  L0=W;
  X0=-W/2;
  stokes = true;
  DT = 0.1;
  TOLERANCE_MU = 1e-5;
  run(); 
}

    The fluid is injected on the left boundary with a velocity U_o.

    u.n[left]  = dirichlet(1.);
p[left]    = dirichlet(0.);
pf[left]   = dirichlet(0.);

u.n[right] = dirichlet(1.);
p[right]   = dirichlet(0.);
pf[right]  = dirichlet(0.);

//u.t[top] = dirichlet(1.);
//p[top]   = dirichlet(0.);
//pf[top]  = dirichlet(0.);

    The sphere is a non-slip surface.

    u.n[embed] = dirichlet(0.);
u.t[embed] = dirichlet(0.);

    Expression of the exact values of the dimensionless radial and azimuthal component of the velocity are:

    double vrad(double x, double y) {
  double theta = atan2(y, x), r = sqrt(x*x + y*y);
  return cos(theta)*(1. + pow(r,-3)/2. -3/(2.*r));
}

    and.

    double vtheta(double x, double y) {
  double theta = atan2(y, x), r = sqrt(x*x + y*y);
  return -sin(theta)*(1. - pow(r,-3)/4. -3/(4.*r));
}

event init (t = 0)
{

    Viscosity is unity.

      mu = fm;
  rho = cm;

    The mesh is initially refined only around the sphere up to LEVEL. The grid is unrefined as the cells are further of the sphere.

      refine ( level <= (LEVEL - sqrt(sq(x) + sq(y))/5.));

    The variables cs and fs characterize just the geometry of the embed solid.

      vertex scalar phi[];
  foreach_vertex()
    phi[] = sq(x) + sq(y) - sq(1.);
  
  fractions (phi, cs, fs);

    We set the initial velocity field.

      foreach() 
    u.x[] = cs[] ? 1.0 : 0.;

    The variables cm and fm gathers either the metric and the embed solid factors. Therefore they must be updated right after the solid factor were updated.

      cm_update (cm, cs, fs);
  fm_update (fm, cs, fs);  
  restriction ({cm, fm, cs, fs});
}

    We check the number of iterations of the Poisson and viscous problems and the convergence to a stationary.

    event logfile (i++) {
  double du= change (u.x, un);
  if (i > 0 && du < 1e-4) {    
    fprintf(stderr, "#du=%g step i=%d\n",du,i);
    return 1;
  }
}

    We produce a snapshot once it is converged…

    event snapshot (t = end)
{
  view (fov = 2, width = 900, height = 900);
  draw_vof ("cs", filled = -1, fc = {1,1,1} );
  squares ("u.y", spread = -1, linear = true);
  mirror ({0,1}) {
    draw_vof ("cs", filled = -1, fc = {1,1,1});
    squares ("u.x", spread = -1, linear = true);
  }
  save("veloc.png");
  
  clear();
  view (fov = 2, width = 900, height = 900);
  draw_vof ("cs", filled = -1, fc = {1,1,1} );
  squares ("p", spread = -1, linear = true);
  isoline ("p");
  mirror ({0,1}) {
    draw_vof ("cs", filled = -1, fc = {1,1,1});
    squares ("p", spread = -1, linear = true);
    isoline ("p");
  }
  save("press.png");
  
  p.nodump = pf.nodump = false;
  dump();
}

/* 
When converged we plot the velocity profiles up to a distance of aprox 4
radius. */

event plotting (t = end)
{
  double alpha = 45*M_PI/180;
  double h  = 4./(99), slope = tan(alpha);
  double xo = cos(alpha);
  for (int i = 1; i <= 100; i++) {
    double x = xo + (i-1)*h, y = slope*x, r = sqrt(sq(x) + sq(y));
    double ux = interpolate (u.x, x, y); // dimensionless velocities
    double uy = interpolate (u.y, x, y);
    double vr, vt; 
    vr = ux*cos(alpha) + uy*sin(alpha);
    vt =-ux*sin(alpha) + uy*cos(alpha);
    fprintf (stdout, "%g %g %g %g %g\n",
	     r, vr, vt, vrad(x,y), vtheta(x,y));
  }
}

event stop (i=500) {}

    Results

    Components of the velocity top: uy bottom: ux

    Components of the velocity top: uy bottom: ux

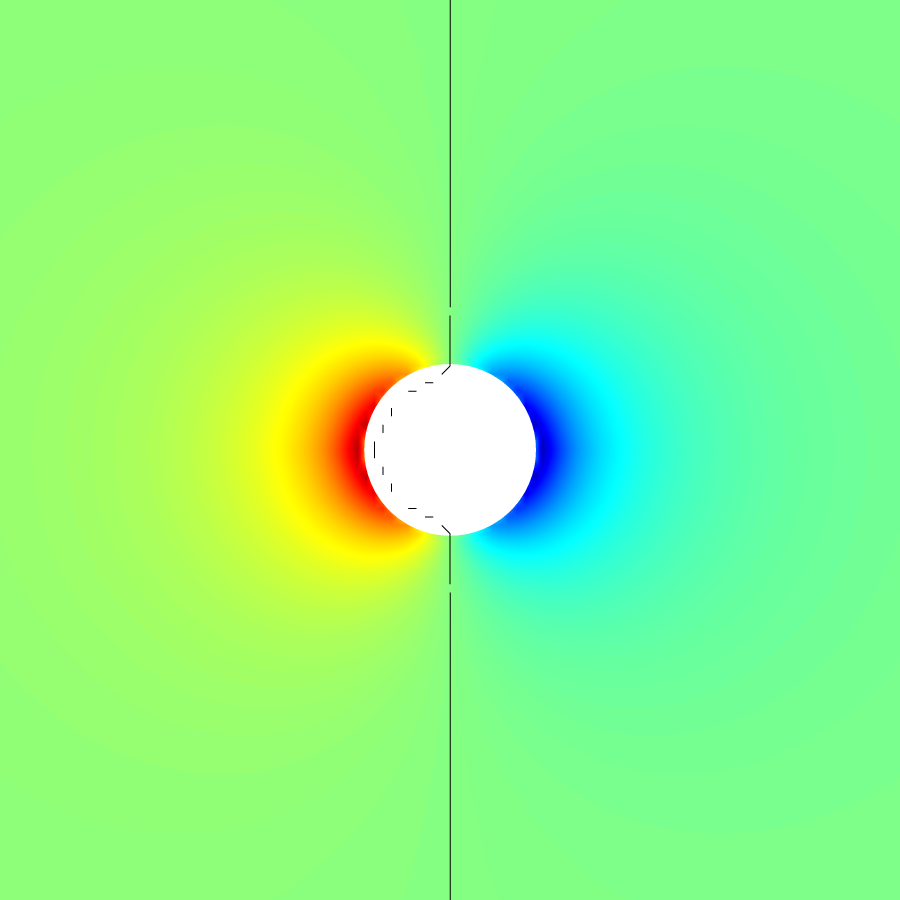
    pressure distribution around the sphere.

    pressure distribution around the sphere.

    reset
set xlabel 'r'
set ylabel 'u_r, u_{/Symbol q}'
set arrow from 15,1 to 165,1 nohead dt 2
plot 'out' u 1:2 t 'u_r (Numerical)', \
  'out' u 1:4  w l t 'u_r (Analytical)',\
  'out' u 1:3 t 'u_{/Symbol q} (Numerical)', \
  'out' u 1:5  w l t 'u_{/Symbol q} (Analytical)'
    (script)

    (script)