porous3D.c

Stokes flow through a complex 3D porous medium

Stokes flow through a complex 3D porous medium

This is the 3D equivalent of the 2D porous medium test case. The medium is periodic and described using embedded boundaries.

This tests mainly the robustness of the representation of embedded boundaries and the convergence of the viscous and Poisson solvers.

#include "grid/octree.h"
#include "../myembed.h"
#include "../mycentered.h"
#include "view.h"

Geometry

The porous medium is defined by the union of a random collection of spheres. The number of spheres can be varied to vary the porosity.

void p_shape (scalar c, face vector f)
{
  int ns = 700;
  coord pc[ns];
  double R[ns];
  srand (0);
  for (int i = 0; i < ns; i++) {
    foreach_dimension()
      pc[i].x = 0.5*noise();
    R[i] = 0.04 + 0.08*fabs (noise());
  }

Once we have defined the random centers and radii, we can compute the levelset function \phi representing the embedded boundary.

Since the medium is periodic, we need to take into account all the sphere images using periodic symmetries.

Note that this means that each function evaluation requires 27 times ns evaluations of the function for a sphere. This is expensive but could be improved a lot using a more clever algorithm.

  vertex scalar phi[];
  foreach_vertex() {
    phi[] = HUGE;      
    for (double xp = -L0; xp <= L0; xp += L0)
      for (double yp = -L0; yp <= L0; yp += L0)
	for (double zp = -L0; zp <= L0; zp += L0)
	  for (int i = 0; i < ns; i++)
	    phi[] = intersection (phi[], (sq (x + xp - pc[i].x) +
					  sq (y + yp - pc[i].y) +
					  sq (z + zp - pc[i].z) - sq (R[i])));
    /* phi[] = -phi[]; */
  }
  boundary ({phi});
  fractions (phi, c, f);
  fractions_cleanup (c, f,
		     smin = 1.e-14, cmin = 1.e-14);
}

Setup

We need a field for viscosity so that the embedded boundary metric can be taken into account.

face vector muv[];

We also define a reference velocity field.

scalar un[];

We will vary the maximum level of refinement, starting from 5.

int lmax = 5;

int main()
{

The domain is 1\times 1\times 1 and periodic.

  origin (-L0/2., -L0/2., -L0/2.);

  foreach_dimension()
    periodic (left);

We set the maximum timestep.

  DT = 2.e-5;

We set the tolerance of the Poisson solver. Note here that we force the Poisson solver to perform at least two cycles. This improves the convergence towards a steady solution for the velocity for high levels of refinement. We also reduce the tolerance of the viscous Poisson solver as the average value of the velocity is around 10^{-6}.

  stokes       = true;
  TOLERANCE    = 1.e-3;
  TOLERANCE_MU = 1.e-7;
  NITERMIN     = 2;

We initialize the grid.

  N = 1 << (lmax);
  init_grid (N);

  run();
}

Boundary conditions

Properties

event properties (i++)
{
  foreach_face()
    muv.x[] = fm.x[];
  boundary ((scalar *) {muv});
}

Initial conditions

event init (i = 0)
{

We set the viscosity field in the event properties.

  mu = muv;

The gravity vector is aligned with the x-direction.

  const face vector g[] = {1., 0., 0.};
  a = g;

We use “third-order” face flux interpolation.

#if ORDER2
  for (scalar s in {u, p})
    s.third = false;
#else
  for (scalar s in {u, p})
    s.third = true;
#endif // ORDER2
  
#if TREE

When using TREE and in the presence of embedded boundaries, we should also define the gradient of u at the cell center of cut-cells.

#endif // TREE

We initialize the embedded boundary.

  p_shape (cs, fs);

We also define the volume fraction at the previous timestep csm1=cs.

  csm1 = cs;

We define the no-slip boundary conditions for the velocity.

  u.n[embed] = dirichlet (0);
  u.t[embed] = dirichlet (0);
  u.r[embed] = dirichlet (0);
  p[embed]   = neumann (0);

  uf.n[embed] = dirichlet (0);
  uf.t[embed] = dirichlet (0);
  uf.r[embed] = dirichlet (0);

We finally initialize the reference velocity field.

  foreach()
    un[] = u.x[];
}

Embedded boundaries

Outputs

We check for a stationary solution.

event logfile (i++; i <= 1000)
{
  double avg = normf(u.x).avg, du = change (u.x, un)/(avg + SEPS);
  fprintf (stderr, "%d %d %d %d %d %d %d %d %.3g %.3g %.3g %.3g %.3g\n",
	   lmax, i,
	   mgp.i, mgp.nrelax, mgp.minlevel,
	   mgu.i, mgu.nrelax, mgu.minlevel,
	   du, mgp.resa*dt, mgu.resa, statsf(u.x).sum, normf(p).max);
  fflush (stderr);

If the relative change of the velocity is small enough we stop the simulation.

  if (i > 1 && (avg < 1e-9 || du < 1e-2)) {

We are interested in the permeability k of the medium, which is defined by: \displaystyle U = \frac{k}{\mu}\nabla p = \frac{k}{\mu}\rho g, with U the average fluid velocity.

    stats s = statsf (u.x);
    fprintf (stdout, "%d %g\n", lmax, s.sum/s.volume);
    fflush (stdout);
        
    char name[80];

We output fields and dump the simulation.

    scalar nu[];
    foreach()
      nu[] = norm (u);
    boundary ({nu});
    
    view (fov = 32.2073, quat = {-0.309062,0.243301,0.0992085,0.914026},
	  tx = 0.0122768, ty = 0.0604286, bg = {1,1,1},
	  width = 600, height = 600);
    box();
    draw_vof("cs", "fs", fc = {0.5,0.5,0.5});
    sprintf (name, "cs-%d.png", lmax);
    save (name);
    
    box();
    isosurface ("u.x", 1e-5, fc = {0.,0.7,0.7});
    sprintf (name, "nu-%d.png", lmax);
    save (name);
    
    view (fov = 19.1765, quat = {0,0,0,1},
	  tx = 0.0017678, ty = 0.00157844, bg = {1,1,1},
	  width = 600, height = 600);
    squares ("nu", linear = true);
    cells();
    sprintf (name, "cross-%d.png", lmax);
    save (name);

We stop at level 8.

    if (lmax == 8)
      return 1; /* stop */

We refine the converged solution to get the initial guess for the finer level. We also reset the embedded fractions to avoid interpolation errors on the geometry.

    lmax++;
    
    adapt_wavelet ({cs,u}, (double[]){1e-2,4e-6,4e-6,4e-6}, lmax);
    
    p_shape (cs, fs);

    boundary (all); // Since boundary conditions depend on volume and face fractions

After mesh adaptation, the fluid properties need to be updated. See event adapt.

    foreach_face()
      if (uf.x[] && !fs.x[])
	uf.x[] = 0.;
    boundary ((scalar *){uf});
    event ("properties");
  }
}

Results

Boundary of the porous medium. Fluid is flowing inside this volume.

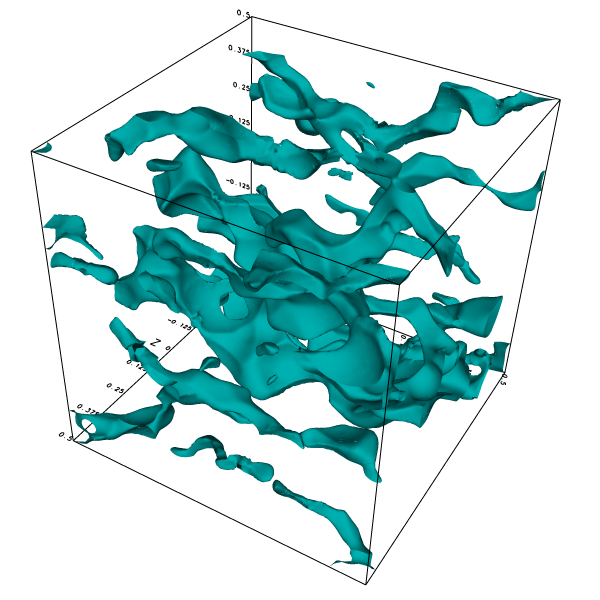
Isosurface of the x-component of the velocity.

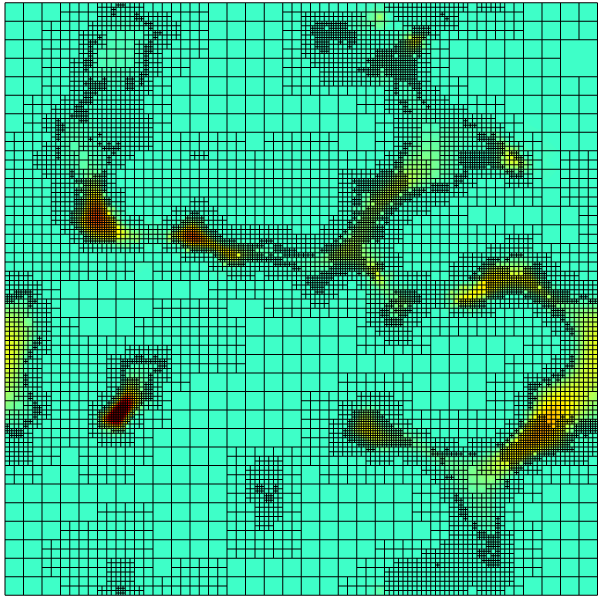
Cross-section at z = 0 showing the mesh and norm of the velocity.

set terminal svg font ",16"
set key top right spacing 1.1
set grid
set ytics format '%.0e'
set xlabel 'level l'
set ylabel 'permeability k'
set logscale y
plot 'out' w lp pt 7 ps 0.7 lc rgb "black" notitle

Permeability as a function of resolution (script)

set terminal svg font ",12"
set key top left spacing 1.
unset grid
set xtics -1000,100,1000
set ytics format '%.0e' 1e-20,1e-4,1e10
set xlabel 'n'
set ylabel ''
set yrange [1e-14:1e6]
set logscale y
plot 'log' u 2:9  w p pt 7  ps 0.7 lc rgb "black"     t '||u_{x}^{n+1} - u_{x}^{n}||_{inf}/||u_x^{n+1}||_1', \
     ''    u 2:10 w p pt 5  ps 0.7 lc rgb "blue"      t '||res_p||_{inf}*dt',  \
     ''    u 2:11 w p pt 2  ps 0.7 lc rgb "red"       t '||res_u||_{inf}', \
     ''    u 2:12 w p pt 12 ps 0.7 lc rgb "sea-green" t '||u_x||_{1}', \
     ''    u 2:13 w p pt 1  ps 0.7 lc rgb "coral"     t '||p||_{inf}'

Convergence history (script)